Matte - Teckenpedagogerna

Positionssystemet

Decimaltal i utvecklad form
\[\space 2769,314=2000+700+60+9+0,3+0,01+0,004\]

Våra tal är uppbyggda på ett positionssystem med talet 10 som bas och som kallas för decimalsystemet. Här lär man sig hur decimalsystemet fungerar.

Addition och subtraktion av bråk

Beräkna \[\space\space\space\space \frac{3}{4}+\frac{1}{2}-\frac{5}{12}\]

MGN med hjälp av multiplikationstabeller.

Beräkna \[\space\space\space\space\frac{3}{4}+\frac{1}{6}\]

MGN med hjälp av primtal

Beräkna \[\space\space\space\space\frac{5}{21}-\frac{3}{14}+\frac{1}{4}\]

Primtal & sammansatta tal - Teori

Vad är ett primtal?

Primtal - Eratosthenes såll.

Aktivitet:
Hitta alla primtal som är mindre än 100 med hjälp av Eratosthenes såll.

PDF: "Eratosthenes såll - primtals detektiven."

Multiplikation av bråk

Beräkna \[\space\space\space\space\frac{5}{7}·\frac{2}{3} \space\space\space \space\space\space\space\space\space\space\space\space 3·\frac{2}{5} \space\space\space\space\space\space\space\space\space\space\space\space \frac{3}{8}·\frac{4}{9}\]

Delbarhetsregler

PDF: "Delbarhetsregler."

Division och omskrivning av bråk - Teori

Skriv om \[\space\space\space\space\frac{\frac{a}{b}}{\frac{c}{d}}\space\space\text{med hjälp av}\space\space\frac{d}{c}\]

Division och omskrivning av bråk - Numerisk exempel

Beräkna \[\space\space\space\space \frac{\frac{2}{5}}{\frac{6}{7}}\space\space\space\text{med hjälp av}\space\space\frac{7}{6}\]

Decimaltalens egenskaper

Ändlig decimalutveckling: \[\space\space\frac{2}{5}=0,4\] Oändlig decimalutveckling kan vara:
1. periodisk \[\space\space\frac{1}{3}=0,3333.....\] 2. operiodisk \[\space\space\pi=3,14159.....\]

Avrundning - avrundningsregler

Avrundningsregler:
Om siffran efter avrundningssiffran är
- 0, 1, 2, 3, 4 står avrundningssiffran kvar
- 5, 6 , 7 , 8 , 9 avrundas avrundningssiffran ett steg uppåt
ex.1
Avrunda till tiotal
a) 57
b) 132
ex.2
Avrunda till två decimaler
a) 12,346
b) 38,1239

Gällande siffror / värdesiffror

Hur många gällande siffror / värdesiffror har följande tal? \[\space\space\space\space\space \text{a)}\space\space 1027\] \[\space\space\space\space\space \text{b)}\space\space 3,470\]\[\space\space\space\space\space \text{c)}\space\space 0,000\space 52\]\[\space\space\space\space\space \text{d)}\space\space 10\space000\]

Från decimaltal till bråk - Teori - fördjupning

ex.1
Skriv 5,333... som ett bråk.

Från decimaltal till bråk - fördjupning

ex 2.
Skriv 14,656565... som ett bråk

Från decimaltal till bråk - fördjupning

ex 3.
Skriv 15,234234234… som ett bråk

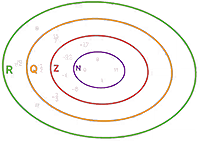
Talmängder