Matte - Teckenpedagogerna

Lös ekvationerna mha potenslagarna

Lös ekvationerna mha potenslagarna

\[\space\space\space\text{ b)}\space\space 4^{3x}=16\]

Del 1 Del 2 Del 3 Del 4

Vad är en potens?

Potens

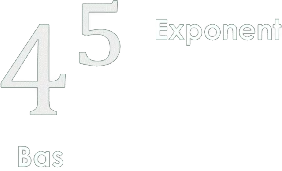
Potenslag 1

\[\space\space\space a^x \cdot a^y=a^{x+y} \]

Potenslag 2

\[\space\space\space\frac{a^x}{a^y} =a^{x-y}\]

Potenslag 3

\[\space\space\space (a^x)^y=a^{x \cdot y}\]

Potenslag 4

\[\space\space\space (a\cdot b)^x=a^x\cdot b^x\]

Potenslag 5

\[\space\space\space\left(\frac{a}{b}\right)^x =\frac{a^x}{b^x}\]

Förenkling av potenser del 1

Förenkla
\[\space\space\space 6^5 \cdot 6^3 \]

Förenkling av potenser del 2

Förenkla
\[\space\space\space\frac{7^8}{7^5} \]

Förenkling av potenser del 3

Förenkla
\[\space\space\space\frac{3^7 \cdot 3^5\cdot 3^4}{3^6 \cdot 3^{9}} \]

Förenkling av potenser del 4

Förenkla
\[\space\space\space \frac{ (4x^2)^3}{16x^4}\]

Förenkling av potenser del 5

Förenkla
\[\space\space\space\left(\frac{1}{3b}\right)^3 \]

Lös ekvationerna mha potenslagarna

\[\space\space\space\text{ a)}\space\space 5^{x-2}=125\]

Lös ekvationerna mha potenslagarna

\[\space\space\space\text{ c)}\space\space 3^x = 27\cdot3^{100}\]

Lös ekvationerna mha potenslagarna

\[\space\space\space\text{ d)}\space\space 5^{x}= 5^{400}+5^{400}+5^{400}+5^{400}+5^{400}\]

Problemlösning potenser 1

Vilket tal är störst
\[\space\space 5^{300}\space\space\space \text{eller}\space\space\space 2^{700}\space?\]

Problemlösning potenser 2

Bestäm x & y om
\[\space\space\space 5^{12}\cdot10^x = 40 \cdot25^y\]

Exponenten noll och negativa exponenter

Vad innebär
\[\space\space\space7^0\space\space\space\text{och}\space\space\space5^{-2}\space?\]

Grundpotensform - repetition teori

Tal i grundpotensform skrivs \[\space\space\space a\cdot 10^n\space\space \text{där}\space\space n \space\space\text{är ett heltal och}\space\space 1≤ a <10\]

Grundpotensform - stora tal

Skriv 150000000000000 mm i grundpotensform.

Grundpotensform - små tal

Skriv 0,000000000001 mm i grundpotensform.

Prefix istället för tiopotenser - teori

Vad är ett prefix och hur används det?

Prefix istället för tiopotenser del 1

Skriv utan prefix.
a) 3,5 kg
b) 3 cm

Prefix istället för tiopotenser del 2 - stora tal.

Skriv 1500000000000 B (byte) med hjälp av prefix.

Prefix istället för tiopotenser del 3 - små tal.

Skriv 0,00000014 m med hjälp av prefix.