Matte - Teckenpedagogerna

Bestäm linjernas k-värde, m-värde och bestäm linjernas ekvationer.

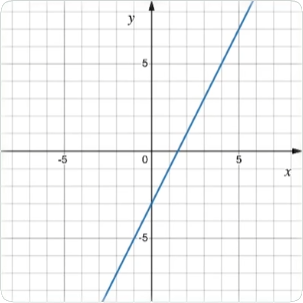
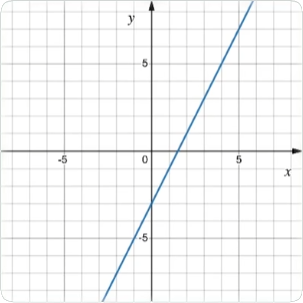
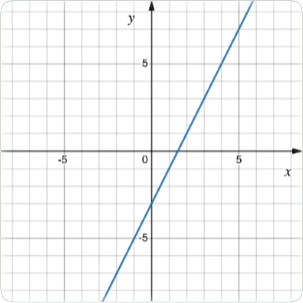
Räta linjens ekvation y = kx + m - teori

Tre fall
\[\space\space\space\space 1.\space\space k>0
\space\space\space \space\space\space\space 2.\space\space k=0
\space\space\space \space\space\space\space 3.\space\space k<0 \]

Bestäm ekvationen för en rät linje som går genom origo och punkten

\[\space\space\space a)\space\space (2,6)\]

Bestäm ekvationen för en rät linje som går genom origo och punkten

\[\space\space\space b)\space\space (-3,12)\]

En rät linje går genom punkten (3,4).

Vilken/vilka av följande punkter (1,5), (-2,-2), (3,-4), (-3,4) & (-1,0) kan ligga på linjen om \[\space\space\space\space a)\space\space k>0 \]

En rät linje går genom punkten (3,4).

Vilken/vilka av följande punkter (1,5), (-2,-2), (3,-4), (-3,4) & (-1,0) kan ligga på linjen om \[\space\space\space\space b)\space\space k<0 \]

En rät linje går genom punkten (3,4).

Vilken/vilka av följande punkter (1,5), (-2,-2), (3,-4), (-3,4) & (-1,0) kan ligga på linjen om \[\space\space\space\space c)\space\space k=0 \]

En rät linje går genom punkten (3,4).

Vilken/vilka av följande punkter (1,5), (-2,-2), (3,-4), (-3,4) & (-1,0) kan ligga på linjen om \[\space\space\space\space d)\space\space \text{linjen saknar lutning?} \]

Bestäm linjens ekvation.

Rita en linje som går genom punkten (-2,5) och har lutningen -2.
Bestäm linjens ekvation.

Bestäm linjernas k-värde, m-värde och bestäm linjernas ekvationer.

Bestäm räta linjens ekvation algebraiskt - teori

1. Bestäm k-värdet. \[\space\space\space k=\frac{\bigtriangleup y}{\bigtriangleup x}= \frac{y_2 -y_1}{x_2 - x_1}\]

Bestäm räta linjens ekvation algebraiskt - teori

2. Bestäm m-värdet.

Bestäm linjens ekvation algebraiskt.

En rät linje med lutningen 3 går genom punkten (2,5).
Bestäm linjens ekvation algebraiskt.

En rät linje går genom punkterna (-10,8) & (4,1).

Bestäm linjens ekvation algebraiskt.

Bestäm x & y så punkterna ligger på en rät linje - algebraisk lösning

a) \[\space\space\space \mathsf{A}=(-3 ,2)\space\space\space\space \mathsf{B}=(1 ,5) \space\space\space\space \mathsf{C}=(x ,8)\]

Bestäm x & y så punkterna ligger på en rät linje - Grafisk lösning

b) \[\space\space\space \mathsf{D}=(-2 ,10)\space\space\space\space \mathsf{E}=(-5 ,y) \space\space\space\space \mathsf{F}=(4 ,0)\]

Parallella linjer - Teori

Två linjer är parallella om och endast om deras k – värden är lika och m – värden är olika.

Vilka av följande linjer är parallella?

\[\space\space \mathsf{A}\space\space\space\space y = -2x-10 \] \[\space\space\mathsf{B} \space\space\space\space 2y +4x = 8\] \[\space\space \mathsf{C}\space\space\space\space 3y = 6x + 12\] \[\space\space \mathsf{D}\space\space\space\space y = 3x - 10\]

Bestäm ekvationen.

Bestäm ekvationen för linjen som går genom punkten (-4,-5) och är parallell med linjen\[\space y = -3x+7.\]

Vinkelräta linjer – teori

Vinkelräta linjer skär varandra med en vinkel på 90° emellan dem. För att linjer ska skära varandra vinkelrätt så krävs att produkten av deras k-värden är lika med -1.
Alltså \[\space\space\space k_{1}\cdot k_{2} = -1\]

Bestäm k.

Bestäm k så att linjerna \[\space \space y=kx + 9 \space\space\space\text{&}\space\space \space y= 5x – 12\] blir vinkelräta.

Är triangeln rätvinklig?

Punkterna (5 ,2),(20 ,-8) & (25 ,25) är hörn i en triangel.
Är triangeln rätvinklig?